Índice del artículo
Desde los primeros meses de vida, los niños comienzan a construir su manera de entender el mundo a través de la exploración. Tocan, observan, comparan, apilan, clasifican… y en cada una de esas acciones están desarrollando los conceptos lógico-matemáticos que les permitirán, años después, comprender relaciones, anticipar resultados y organizar su pensamiento.
Y te encantará saber que estos aprendizajes no requieren fichas ni ejercicios formales. Nacen del juego, de la curiosidad natural y de la interacción con los adultos y el entorno. De hecho, las matemáticas se construyen mucho antes de que aparezcan los números: cuando el bebé reconoce que un objeto es más grande que otro, que algo está dentro o fuera, que su plato se ha quedado vacío, o que una actividad ocurre siempre después de otra en una rutina.
Comprender y acompañar este proceso nos permite ofrecer experiencias ricas y significativas que fortalecen su desarrollo cognitivo. En este artículo vamos a descubrir cómo surgen y evolucionan los principales conceptos lógico-matemáticos desde el nacimiento y durante la infancia temprana.
Conceptos lógico-matemáticos base
¿Cómo se acercan los bebés a lo que, más adelante, los niños mayores y los adultos entendemos como matemáticas?
Desde prácticamente el nacimiento, los niños comienzan a construir conocimientos a través de sus experiencias cotidianas. Muchas de ellas están directamente relacionadas con los conceptos lógico-matemáticos, que no solo les preparan para comprender las matemáticas en el futuro, sino que también les ayudan a desenvolverse mejor en su vida diaria.
Acercar a los más pequeños a estos conceptos desde edades tempranas favorece un pensamiento más estructurado, una mayor capacidad de observación y una comprensión más profunda del entorno que los rodea.
El concepto de cualidad: descubrir las propiedades de los objetos desde bebés
Una cualidad es un atributo, propiedad o característica, un adjetivo, vamos.
En primeras edades, nos valemos de la manipulación de los objetos cotidianos, experimentando sus cualidades de manera natural, a partir de los sentidos.
Conforme el niño crezca, comenzará a identificar, definir y reconocer cualidades físicas como el color, la temperatura, la forma, el sonido, el tipo de material, el grosor, la consistencia…

En un primer momento, el niño nos dirá que la estrella es roja y la naranja, redonda. Más adelante, nos sorprenderá indicando que la estrella pincha (o que tiene muchas puntas) y que la naranja huele bien.
Primero se dan acercamientos más básicos, inmediatos, fácilmente reconocibles y, después, el niño, conforme gana experiencia sensorial, discrimina cualidades más complejas.
Así, el reconocimiento de formas y tamaños en bebés se da por percepción sensorial, considerando exclusivamente lo que se ve, lo que se toca.
Con ello aparece, meses después, la capacidad de agrupar los elementos a partir de dichas cualidades; primero discriminando una sencilla, luego alguna más compleja, más tarde lo podrá hacer con dos y así sucesivamente.
Alternando material didáctico con aquel de elaboración propio y también objetos cotidianos, multiplicamos la riqueza de las experiencias del bebé desde sus primeros meses de vida, potenciando la asimilación posterior del resto de conceptos lógico-matemáticos y favoreciendo el proceso de pensamiento.
En edades tan prontas, se debe dejar que el niño utilice los recursos cuando y como quiera, permitiendo que les dé más de una finalidad (aunque, de hecho, ninguna sea la que esperamos). nosotros simplemente acompañamos, motivamos y ayudamos si es necesario.
El concepto de cantidad en los bebés: primeras nociones lógico-matemáticas
Podemos empezar a hablar de pensamiento lógico-matemático en bebés con el concepto de cantidad. Y, curiosamente, se da bastante pronto.
En la infancia temprana, los peques serán capaces de trabajar con los extremos mucho y poco, nada y todo, más y menos y discriminar solo «un poco».
El entorno ofrece muchas posibilidades para que experimentemos con las cantidades. Este concepto puede surgir con el juego libre, si bien, suele ocurrir antes, con una actividad cotidiana tan básica como es la alimentación complementaria.
Sin darnos cuenta, nuestro bebé es quien nos invita a hablar de cantidad cuando, introduciéndose a sí mismo en el baby sign, nos pide más comida.
Os cuento una anécdota de mi hijo:

Con este ejemplo propio queda de manifiesto que, en edades muy tempranas, no se diseñan actividades específicas de cuantificación. Lo ideal es optar por aquellas que facilitan la observación y la manipulación, incluyendo situaciones que puedan dar lugar a experiencias cuantificadoras de manera secundaria mientras buscan otro objetivo principal.
Fases de adquisición y dominio de cantidad desde el nacimiento
Esta adquisición requiere de una serie de aproximaciones que se dan de manera secuencial.
- Se disfruta de sensaciones a través del tacto. El bebé debe tocar elementos externos pero también su propio cuerpo.
- Experimentación con materiales de las mismas cualidades. Con ello se puede trabaja «mucho», «todos», «nada», «uno», «un poco»…
- Reconocimiento de las partes del cuerpo.
- Experimentación con materiales que tienen alguna diferencia en alguna de sus cualidades. Introducimos «estos son diferentes», «estos y aquellos», «más que…».
- Los adultos cuantificamos nuestras acciones.
- Pedimos al niño una cantidad de cualquier cosa.
- Instamos a que verbalice la cuantificación.
Cómo se desarrolla el concepto de número en la primera infancia
Es común ver, desde muy pequeños, cómo los niños manifiestan nociones de número. Son típicas la imagen de un niño que sabe que tiene un añito y te lo sabe decir sacando un dedo o la de un niño que aún no cumple los tres años y recita el «guanchufrí«.

Pero, por supuesto, esto no significa que sepan lo que dicen y, mucho menos, de manera específica. Se está aplicando un esquema intuitivo sin que esté asumida la concepción de cantidad ni, mucho menos, de número.
Antes de poder trabajar este último, los peques deben manejar con soltura los cuantificadores para designar cantidades, pero sin especificar.
De nuevo, el modo más inteligente, eficiente y natural de trabajar los números en bebés es con actividades en las que se favorezca la estructuración de esta idea de número.
Al clasificar de tantas formas como sea posible, el niño terminará eligiendo, de manera espontánea, el número como criterio para conseguirlo.
Lo importante es calcular mediante aproximación. Después, el niño comprobará si el cálculo es correcto estableciendo una relación término a término (correspondencia). Este tipo de ejercicio se realizará, en sesiones diferentes, hasta que la estimación sea correcta.
Los peques conseguirán, con relativa facilidad, ordenar grupos preconstituidos con una cantidad de elementos. Un par de meses después ya deberían ser capaces de formar grupos con más (o menos) elementos que el grupo inicial (sin determinar número).
❗❗❗ DISCLAIMER ❗❗❗
Los niños creen que lo que se ve más grande realmente lo es.
Si analizamos una fila de 4 caramelos distanciados a 2 centímetros unos de otros y otra fila con 5 caramelos distanciados a solo 1 centímetro unos de otros, creerán que en la primera fila, de 4 caramelos, hay más, sólo porque abultan más.
En el periodo preoperacional estamos muy unidos a la percepción de la realidad que tenemos.
Entender el concepto de número implica entender a su vez:
- La relación de correspondencia uno a uno. Se establece que dos conjuntos cualquiera son equivalentes en número si a cada uno de los objetos que los componen le corresponde otro. Esta es una definición obvia para nosotros pero que puede ayudar mucho al niño a la hora de acercarse al concepto de número.
- La conservación. Si hay dos conjuntos iguales, no importa cómo los coloquemos, siempre existirá en mismo número de objetos componentes.
Por esto mismo, es especialmente importante verbalizar lo que hacemos, en particular, cuando contamos. Por supuesto, lo haremos, también, con todas las relaciones establecidas, denominarlas correctamente y evocar, a posteriori, las actividades que hemos hecho.
El concepto de medida: comparar, estimar y descubrir el entorno
La medida es una comparación de cantidades de una misma magnitud, siendo una de ellas, escogida arbitrariamente, la que funciona como unidad.
Con la manipulación constante, realizamos comparaciones de volumen, de longitud, de peso… siempre a nivel perceptivo (lo cual, recordemos, no siempre resulta correcto, pues es algo, además, totalmente subjetivo).

Este es otro de los conceptos lógico-matemáticos con los que los peques presentan «problemas». Y, es que, de manera similar al disclaimer anterior, tenemos que, cuando los niños comienzan a entender de cantidad, no son capaces de entender esa conservación de la que hablábamos.
Como ejemplo, el que ya expliqué en el post sobre cómo se desarrollan los conceptos lógico-matemáticos desde bebés. Enseñamos a un niño dos vasos, uno corto y ancho y otro largo y delgado, los dos con 150 ml de agua. Sin dudar, el niño te asegurará que en el último hay más porque su percepción (a través del sentido de la vista) le dice que el agua llega hasta más arriba, que lo llena más.
De hecho, podrías mostrarle un trasvase del agua del primer vaso al segundo y seguiría diciéndote que hay más en el largo. Como ya dije: para el niño tiene más sentido que el agua se multiplique al verterla que el hecho de que cambie su forma en función del recipiente. Tiene más sentido que el agua sea infinita (por ejemplo, porque la ven salir del grifo sin parar o porque ven que el mar no tiene fin o que el río corre sin cesar) a que pueda adaptarse al vaso (no tiene vida).
Hasta que no entienda el concepto de conservación, el peque seguirá pensando que nos hemos sacado el agua de la manga para llenar «más» el vaso de tubo.
Lo mismo ocurrirá si le damos dos piezas de metal de cierto peso, por ejemplo, 50 gramos. Las dos tienen forma de pastilla. El diámetro de una de ellas es de 5 cm mientras que el de la otra es de 3 cm. El niño pensará que pesa más la primera, incluso teniendo una en cada mano para comprobarlo.
Durante los primeros años, los peques aprenderán sobre las medidas a partir de nociones básicas y contrastadas de elementos mesurables (mucho/poco, todo/nada, redondo/cuadrado, grande/pequeño, ligero/pesado…, por comparación de tamaños/formas, básicamente). Esto es, debe existir un claro contraste perceptivo que no dé lugar a duda. El niño debe diferenciar dos objetos como contrarios a partir de una comparativa de una característica dada.
El concepto de espacio en los niños pequeños: orientación y percepción
Para Dienes, el concepto de espacio no se enseña. Lo que tenemos que hacer es crear y presentar situaciones y experiencias que ayuden a formarlo mentalmente, buscando que este pueda ser, valga la redundancia, un espacio correcto donde enmarcar lo que le sucede de manera objetiva. Es decir, el adulto tratará de conseguir que el niño adquiera un concepto de espacio ajustado y objetivo para que sus experiencias también lo sean, resultando más fáciles de aprender.
El espacio en relación al propio cuerpo
Todas las nociones espaciales de orientación, situación y distancia están, en principio, relacionadas con el esquema corporal y la motricidad de uno mismo.
Para orientarse, el niño necesita hacer comparaciones y medidas respecto a su cuerpo así como encontrarse los puntos relacionados con las tres dimensiones (arriba y abajo, delante y detrás y a un lado y al otro).
Reconocer y situar los objetos de su entorno y su relación con ellos permite a los niños obtener una orientación espacial. Como es lógico, conformen crecen, su capacidad para situar los objetos, mejora. También comienza a construir el espacio mentalmente, organizándolo, lo que supone un gran salto en su conocimiento espacial y también sienta la base de su posterior conocimiento en geometría.
La organización del espacio y los materiales
Al respecto, lo que debemos procurar los adultos es que los espacios en los que nuestro peque interactúe constantemente sean ricos en estímulos, potenciadores del desarrollo, capaces de propiciar todo conocimiento. Buscamos una buena organización, accesibilidad de los juegos y juguetes y disposición de materiales variados y acordes a los objetivos que tengamos en cada momento (guardando lo que no nos sea de utilidad).
Conceptos lógico-matemáticos básicos de espacio
Obviando las relacionadas con su cuerpo, encontramos algunas nociones que los niños descubren, de hecho, desde muy temprano.
Conceptos lógico-matemáticos de:
- Orientación estática. Delante/detrás, a un lado/a otro lado y arriba/abajo.
- Direccionalidad. Saliendo del cuerpo, deben saber expresar lo que está hacia arriba, delante…
- Situación de los objetos en el espacio. Reconocer su posición y distancia respecto a otro elemento.
- Dimensionalidad. A los 3 años, los peques deben discernir si una imagen es, o no, tridimensional.
- Cierre. Igualmente, debe reconocer el cuerpo de las líneas, definiendo su final y su cierre, si lo tienen.
- Topología. El niño discriminará, antes de los dos años, lo que está dentro de lo que está fuera y lo abierto o cerrado, aunque no lo exprese con palabras hasta bastante después.
El concepto de tiempo: entender la secuencia de los acontecimientos
El último de los conceptos matemáticos tempranos que adquiere un niño es el tiempo.

Los niños interiorizan el tiempo a partir de las actividades cotidianas y las rutinas que les enseñamos. Sin ellas, están perdidos en el día hasta que se va el sol, se sienten inseguros, no pueden prever, tendrán dificultades para adquirir un ritmo… ¡Fíjate si son importantes!
No sera hasta los tres años que tu peque se empiece a interesar por medir el tiempo, coincidiendo con su capacidad para poder hacerlo. Es en este momento cuando entiende cómo puede conseguirlo utilizando recursos que funcionan como elementos de medida, los cuales percibe con los sentidos y desentraña cognitivamente.
Hasta este momento, el papel del adulto es esencial, pues será el que pueda introducir nociones temporales para que, al llegar a esos tres añitos, tengamos niños capaces. Lo haremos, simplemente, verbalizando nuestras acciones. «Nos bañamos después de merendar», «Jugamos cuando hayamos terminado de comer», «Ahora estamos llegando a casa»…
De nuevo, el niño entiende todo esto mucho antes de poder expresarse al respecto, por lo que no hay que dormirse en los laureles. Mi consejo es, de hecho, que lo hagas desde el nacimiento.
En cuanto a la interiorización activa del concepto de tiempo, no dudes en introducir, también, otros aspectos que se le relacionen, como el de velocidad.
Tabla conceptos lógico-matemáticos base
| Concepto | Definición / Idea central | Desarrollo (0-3 años) | Ejemplo |
|---|---|---|---|
| Cualidad | Atributo, propiedad o característica de un objeto. | Manipulando objetos cotidianos y explorando con los sentidos. Primero, color o forma; más tarde, textura, olor, temperatura, etc. | “La estrella es roja”, “La naranja es redonda”, “La estrella pincha”, “La naranja huele bien”. |
| Cantidad | Percepción de la magnitud o número de elementos. | Surge de experiencias sensoriales y cotidianas (alimentación, juego libre). Se comprenden primero los extremos: mucho/poco, todo/nada, más/menos. | El bebé pide “más” comida; distingue entre “pocos” bloques y “muchos” bloques. |
| Número | Representación simbólica de una cantidad. | Antes de contar, el niño clasifica y estima cantidades. Aprende correspondencia uno-a-uno y conservación. El número se integra tras dominar la noción de cantidad. | Sabe que tiene “un año” y muestra un dedo, aunque aún no comprende el valor numérico. |
| Medida | Comparación de cantidades de una misma magnitud (peso, longitud, volumen…). | Se trabaja perceptivamente: comparar lo que parece más grande, largo o pesado. Se consolidará más tarde con la noción de conservación. | Cree que hay más agua en un vaso alto y delgado que en uno bajo y ancho, aunque contengan lo mismo. |
| Espacio | Relación entre objetos, personas y el propio cuerpo en el entorno. | A partir del esquema corporal y la motricidad. Aprende nociones de posición, dirección y distancia. | Comprende “arriba/abajo”, “delante/detrás”, “dentro/fuera”, y orienta objetos en función de sí mismo. |
| Tiempo | Sucesión y duración de los acontecimientos. | A través de rutinas y verbalizaciones del adulto. Alrededor de los tres años empieza a medir el tiempo con referentes perceptivos. | “Nos bañamos después de merendar”, “Jugamos cuando lleguemos a casa”. Aprende a anticipar momentos del día. |

Relaciones operacionales para trabajar los conceptos lógico-matemáticos
¿De qué maneras podemos relacionar los conceptos lógico-matemáticos base que acabamos de ver?
Colecciones: agrupar objetos por una cualidad común
Una colección es un conjunto de objetos que comparten una misma cualidad. Se trata de la forma más teórica del concepto, los objetos no tienen que estar juntos necesariamente para formar parte de una colección, pero la colección sí debe llevar nombrada una cualidad o atributo.
Por ejemplo, tengo una colección de libros de historia; todos están en la estantería a excepción de dos, que llevo en el bolso y en el coche. Aun así, esos dos siguen formando parte de la colección.

Agrupaciones: cómo los niños organizan su entorno
La agrupación nace de un ejercicio mental que se da a partir de la manipulación, la palabra y la imaginación. Es la reunión física de los objetos que tienen atributos en común, lo que haces con las colecciones (y con objetos que no formen parte de una).
Por ejemplo, vamos a agrupar todos los libros de historia; entonces, dejan de estar repartidos en la estantería, el bolso y el coche para dejarlos todos juntos, agrupados.
Otra manera de ver muy clara la diferencia es que vamos a agrupar, por ejemplo, los objetos redondos. En este grupo vas a meter tanto la pelota de playa que pertenece a la colección de «cosas para jugar en la playa», como una naranja.

Se comienza haciendo agrupaciones por cualidades, que aparecen al reconocer las cualidades. Después, se podrán agrupar elementos a partir de relaciones cuantitativas.
Agrupaciones por cualidades o atributos
En primera instancia los niños comienzan a agrupar los objetos por sí mismos, generalmente eligiendo algo que les gusta o que resulta llamativo. Esto es, hablamos de espontaneidad. Las primeras veces suele ser por un tamaño descaradamente grande o, casi siempre, por la sensación táctil que le transmite algo. Este es el motivo por el que los dudus son suaves, por ejemplo.
De esto, podemos deducir que, curiosamente, las primeras agrupaciones espontáneas que hace tu hijo no van a ser, ni de lejos, de objetos parecidos. Y, más curioso todavía, si atendemos a la definición, son agrupaciones correctas.
Cuando el niño comienza a hacer agrupaciones de manera consciente, sigue una secuencia:
- Agrupación por intuición. Escoge los objetos más afines entre sí, los que más se parecen, los que más características físicas evidentes presentan, siguiendo el criterio de máxima similitud.
Este no siempre es constante en el atributo, lo que significa que puede escoger 3 objetos por su color, 2 por su forma, etc. Con el montón de objetos, el peque sabe cuáles ha discriminado y por qué.
Como ejemplo, puede haberse hecho con siete bolas y cuatro peluches. Técnicamente, no es una agrupación correcta, aunque las partes sí lo son.
- Agrupaciones grandes con mismo criterio de similitud. El niño pone su foco en una cualidad (podemos pedírsela nosotros perfectamente) y la reconoce en todos los objetos que tiene a su alcance, discriminándolos y consiguiendo hacer agrupaciones de gran tamaño con los objetos que cuentan con ese atributo y sin incluir, como en el estadio anterior, otros objetos similares en una segunda característica; se centra.
Destacar que aún no encuentra una relación de diferencia entre los objetos, que se han agrupado siguiendo un criterio más amplio.
Del ejemplo, si le da por el color amarillo, soltará una bola azul, una verde y, posiblemente, una color amarillo fluorescente «por error (para el adulto, que entendemos que esa también es amarilla)».
- Discriminación interna. Si se lo pedimos, dentro de una agrupación establecida previamente por él, irá discriminando los objetos atendiendo a características diferentes a la que sirvió de nexo. Hará, con todos ellos, pequeños grupos, correctos, que cumplan con las demandas pedidas.
Ahora, si hablamos con él, verá que dentro del grupo, aunque todo lo que se ha quedado es amarillo, hay cosas tan dispares como una bola de madera y un peluche supersuave.
- Reflexión de la discriminación. Necesitará un poco de experiencia en actividades de discriminación interna para terminar dándose cuenta de que muchos de esos objetos de su colección inicial, escogidos por una característica, tienen otras características en común (y otras, diferentes).
Aquí sí se da cuenta de que, del montón que tiene, unos son peluches y otros son bolas, y entiende que deberían pertenecer a dos agrupaciones diferentes.
Tabla resumen agrupación por cualidades
| Etapa de agrupación | Descripción | Ejemplo |
|---|---|---|
| Agrupación por intuición | Elige objetos que percibe como similares, aunque los criterios puedan variar (color, forma, tamaño). No siempre mantiene una coherencia en el atributo elegido. | Siete bolas y cuatro peluches: agrupación mixta según similitud general. |
| Agrupaciones grandes con mismo criterio de similitud | Centra su atención en una sola cualidad y agrupa los objetos que la comparten, sin mezclar otros atributos. Aún no percibe diferencias dentro de los grupos. | Selecciona solo objetos amarillos, dejando fuera otros tonos parecidos como el amarillo fluorescente. |
| Discriminación interna | Dentro de una agrupación ya creada, comienza a subdividir los objetos en nuevos grupos según características distintas. | Distingue dentro del grupo amarillo una bola de madera y un peluche, reconociendo su diferencia material. |
| Reflexión de la discriminación | Comprende que los objetos de una misma agrupación pueden tener otras cualidades en común o diferentes, entendiendo así la relación entre categorías. | Comprende que del grupo amarillo, unos son peluches y otros bolas, por lo que deberían pertenecer a grupos distintos. |
Agrupaciones por relaciones cuantitativas
Un paso más allá va la agrupación que atiende a una similitud o diferencia cuantitativa.
- Primeramente debemos trabajar con agrupaciones de cantidades incontables (mucho, poco, nada).
- Acto seguido, daremos al niño números, muy separados, para pedirle que ordene los grupos de menor a mayor o viceversa. Aunque no sepa contar, sabiendo que 1 es poco y 9 es mucho, debe saber colocarlos en los extremos. Se trata de que perciba dónde hay más y dónde hay menos. Primero se ordenarán grupos ya formados y después serán ellos quienes formen agrupaciones, primero de muchos y pocos objetos y, después, ya en segundo ciclo de Infantil, de más o menos objetos que el grupo inicial.
- Finalmente, los peques sabrán verbalizar lo que van haciendo, denominando correctamente las relaciones que establecen y siendo capaces de evocarlas más tarde.
Comparar: la base del pensamiento lógico
Visualizar los elementos para detectar sus cualidades y establecer relaciones de similitud y diferencia. Se trata de un proceso mental que lleva a tomar decisiones para clasificar, seriar, etc.

Relaciones
Es el fruto de una comparación en la que se termina por descubrir si los objetos analizados tienen cualidades iguales (o no).
Primero podrán establecer relaciones con un par de objetos dentro de una misma colección y, después, serán capaces de relacionar cualidades más «difíciles», de objetos de distintas colecciones.

Podemos volver al ejemplo anterior. El niño va a ver tanto una naranja como una pelota de playa y va a relacionarlos por su forma. Sin embargo, si ve un cubo de arena y una pelota de playa, sabrá que ambos pertenecen a la colección de objetos de playa.
Con dos años, el niño puede darte otro objeto redondo después de realizar la relación. Con tres años, será capaz de darte otro objeto de la misma colección de playa, después de establecer la segunda relación. Esto ocurre así como es más sencillo que relacionen objetos por sus atributos físicos (forma) que por su utilidad; para esto último necesitan bastante más tiempo.
Clasificar: poner junto lo que se parece

Clasificar es la acción que realiza el pequeño cuando discrimina entre los objetos, agrupándolos según la condición dada.
Primero podrá clasificar por igualdad y, poco después, objetos distintos que tengan una característica común evidente (grandes o rojos, por ejemplo). Cerca de los 3 años podrá discriminar haciendo grupos con elementos de características muy distintas (como animales).
Correspondencia
Es una asociación que se da con correspondencia uno-a-uno. Un objeto o persona se relaciona con otro. Se da una relación término a término. Se da por emparejamiento (iguales) o por asociación (agrupables por alguna variable).
Con ello, el niño empieza a saber si hay un número de cosas igual o diferente; así aparece lo que, en la primera infancia más se aproxima a la matemática que los adultos conocemos.
Ordenar
Tras tomar un atributo como referencia, colocar los objetos que lo contienen según una relación de orden (de grande a pequeño, de pesado a ligero, de mayor a menor, de frío a caliente…).
Seriaciones
Son organizaciones de elementos que se realizan siguiendo patrones y secuencias simples entre las clases existentes, considerando sus diferencias.

Se pueden hacer con objetos que cambien una variable al completo (por ejemplo, secuencia de rojos-azules) o bien considerando un atributo que cambia en grado o matiz.
Tabla resumen relaciones entre objetos
| Concepto | Idea clave | Ejemplo simple |
|---|---|---|
| Colecciones | Conjunto de objetos con una misma cualidad, aunque estén separados. | Colección de libros de historia (aunque algunos estén en distintos lugares). |
| Agrupaciones | Juntar físicamente objetos con un atributo común. | Juntar todos los libros de historia o todos los objetos redondos. |
| Comparar | Observar y detectar similitudes o diferencias entre objetos. | Ver que una pelota y una naranja son redondas. |
| Relaciones | Conclusión de la comparación: descubrir qué cualidades comparten o no. | Pelota y naranja → misma forma. Pelota y cubo → misma colección (juguetes de playa). |
| Clasificar | Separar o agrupar según una condición o criterio. | Clasificar por tamaño, color o tipo de objeto. |
| Correspondencia | Emparejar un objeto con otro (uno a uno). | Repartir una manzana por cada plato. |
| Ordenar | Colocar en secuencia según un atributo. | De grande a pequeño, de claro a oscuro, de frío a caliente. |
| Seriaciones | Crear un patrón o secuencia regular. | Rojo-azul-rojo-azul o piezas de menor a mayor. |
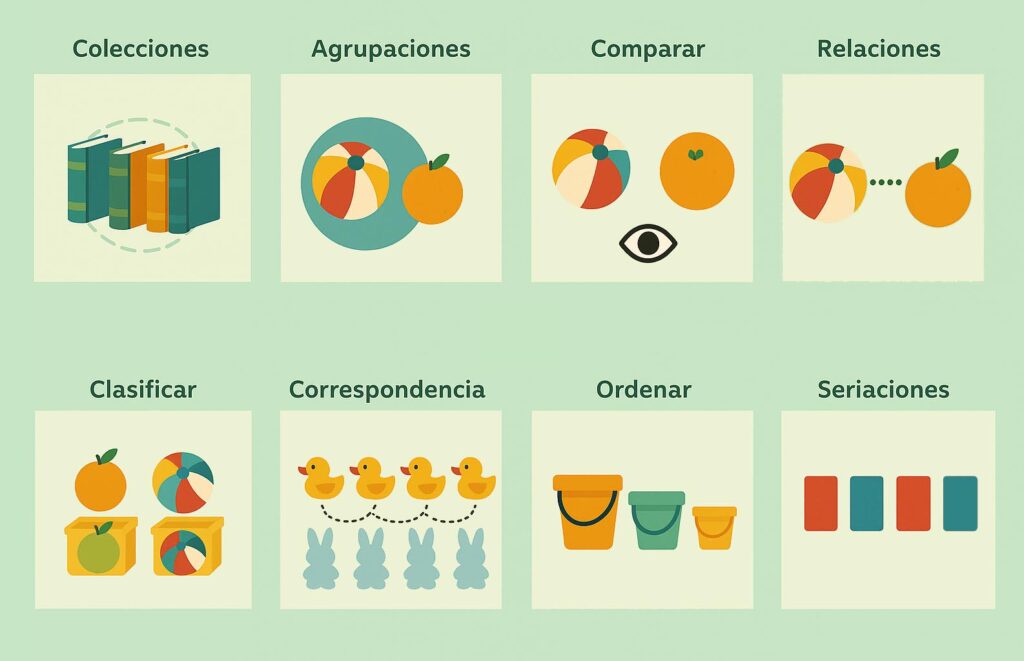
¡Descarga aquí 👇mi ficha-resumen gráfica sobre RELACIONES OPERACIONALES EN BEBÉS!
Actividades para trabajar los conceptos lógico-matemáticos en bebés y niños pequeños
A lo largo de este recorrido hemos visto cómo los bebés y los niños pequeños se aproximan, de manera natural, a los conceptos lógico-matemáticos: cualidad, cantidad, número, medida, espacio y tiempo.
Estos conceptos son la base del pensamiento lógico y de la comprensión matemática posterior, pero también de la manera en que los niños entienden, organizan e interpretan su entorno desde sus primeros meses de vida.
El juego libre, la exploración sensorial y la interacción con el adulto son las herramientas más poderosas para asimilar estas nociones, mucho antes de que aparezcan los números o las operaciones. Sin embargo, hay infinidad de recursos que podemos ofrecer a nuestros peques para adquirir, desarrollar e interiorizar todos estos conceptos.
Puzzles, bloques, pinzas, la propia organización de los juguetes, diseño de patrones y secuencias. Si quieres saber cómo diseñar actividades para trabajar los conceptos lógico-matemáticos, cómo benefician a los niños y tener cientos de ideas, ¡sigue este enlace! 👉
Conclusión: Los conceptos lógico-matemáticos como base del pensamiento y la vida diaria
Los conceptos lógico-matemáticos no son una enseñanza formal, sino una forma de pensamiento que se construye día a día. Desde el momento en que el bebé observa, compara, manipula o anticipa, ya está desarrollando su lógica interna.
Nuestro papel como adultos es favorecer ese pensamiento: ofrecer entornos ricos, materiales variados y rutinas que le permitan experimentar con las nociones básicas del mundo que lo rodea, lo que resulta en una educación matemática temprana natural y ajustada.